Complete Guide To Graphs

Graph Data Structure

Graph is a non-linear data structure defined as a collection of vertices(nodes) and edges(links). The edges in a graph are used to connect the nodes. The nodes in the graph can be used to store data. Each edge of the graph can also store data in the form of weights as we will see below

A graph is represented as G = (V, E) where,

• V is the set of vertices or nodes
  • E is the set of edges in the Graph G . It is represented as ordered pairs of vertices (i,j)

Example :

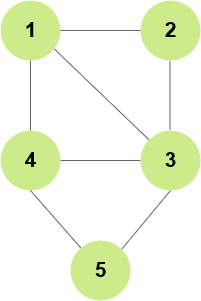
Here:

V = {1, 2, 3, 4, 5}
E = {(1,2), (1,3), (1,4), (2,3), (3,4), (3,5), (4,5)}

For the purpose of coding interviews, we will only consider Simple Graphs (definition given below)

Types of Graphs

Simple Graph

A simple graph is a graph which satisifes two conditions :

1. No self loops: A self loop is defined as an edge from the node to itself. A simple graph does not contain any self loops.
2. No multiple edges: There cannot be multiple edges between two nodes. For example, if there is already an edge b/w node A and node B, there cannot be another edge in the same direction b/w node A and node B.

For the purpose of coding interviews and this tutorial, we will only consider simple Graphs.

Undirected Graphs

Undirected graph is a graph in which the edges don't have a fixed direction. For example, in the below graph the edge b/w node A and B can be used to traverse from both A to B as well as from B to A. Therefore, it is an undirected graph.

Directed Graphs

A graph in which all the edges have a fixed direction is called as a directed graph. For example, in the below graph the edge b/w node A and B can be only used to traverse b/w node A to node B and not the other way round. This is because the edge originates at node A and terminates at node B.

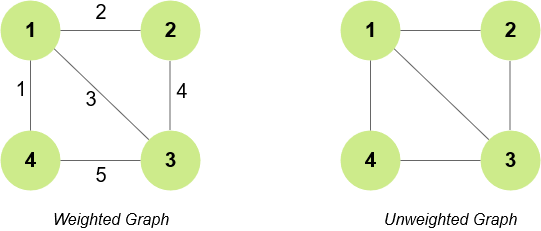
Weighted Graphs

A weighted graph is a graph in which the edges will have weights with them. For example, in the graph given below you will see a number on top of the edges which represents the weight of that edge.

Unweighted Graphs

An unweighted graph is a graph in which the edges don't have any weight associated with them. You can also consider all of the edges to have a weight of 1 in an unweighted graph.

Binary Weighted Graphs

Binary weighted graphs are a special case of weighted graphs in which each edge will have zero or one weight.

Cyclic Graph

A cyclic graph is a graph which can contain a cycle within itself.

Directed Acyclic Graph

A directed acyclic graph is a graph which is a directed graph as well as it cannot contain any cycle. Directed acyclic graphs are used a lot with problems involving topological sorting.

Connected Graph

A connected graph is a graph where there is a path from each node to any other node.

Disconnected Graph

A disconnected graph is a graph where there maybe certain nodes which are not reachable from other nodes. Opposite of connected graphs.

Graphs Implementation

In this section we will cover the ways in which we can implement graphs in code. The graph implementations covered below can be used to implement both directed as well as undirected graphs. They can also be used for implementing both weighted as well as unweighted graphs. There are majorly two ways to represent graphs

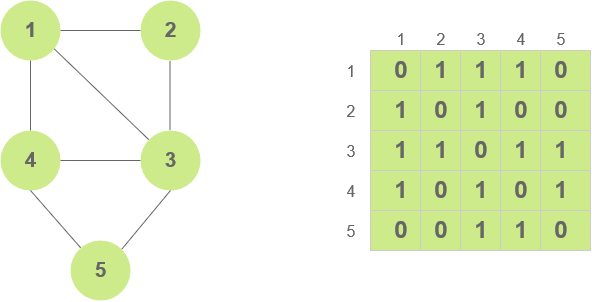
Adjacency Matrix

An adjacency matrix is a 2D array of V x V vertices. Each row and column represent a vertex. ith row in a adjacency matrix represents the edges originating from node i. Similarly, ith column in an adjacency matrix represnets the edges incident towards node i

a[i][j] = 1 – If there is an edge originating from node i to node j a[j][i] = 1 - if there is an edge originating from node j to node i

a[i][j] = 0 – If there is no edge originating from node i to node j a[j][i] = 0 - if there is no edge originating from node j to node i

Since the graph creates a matrix of size V*V, with each cell storing a number, it ends up using O(V*V) space. This is one downside of the adjacency matrix where it ends up using V*V space even if no of edges are less. Therefore, it should not be used for sparse graphs

Adjacency List

Unlike adjacency matrix, adjacency list is a more optimized way of storing the graphs. In this representation, we create an array of linked lists where each linked list represents the edges originiating from the corresponding node.

For example, if there are 5 nodes in the graph there would be 5 linked lists, with the 0th linked list stores the vertices to which the edges originate from node 0, 1st linked list represents the vertices to which the edges originate from node 1 and so on.

Here, the total space used is O(V + E). This is because even if there are no edges, we end up creating V empty lists which would take up at least V space. Each edge will be added in the corresponding linked list (at least once for directed graphs and at most twice for undirected graphs).

What is graph traversal ?

Graph traversal refers to the order in which you will visit all the nodes of a graph. Unlike an array, which is a linear data structure and can be traversed either left to right or right to left , a graph can be traversed in multiple different ways.

The order in which we traverse the nodes of a graph is extremely important and gives rise to various different applications and graph algorithms.

Breadth First Search (BFS)

Breadth First search is a powerful algorithm which is used for traversing and searching within a graph or even a tree.

BFS is the most common graph traversal algorithm which you can apply on a graph. The core idea behind BFS is to explore the nodes in the order of their distance from the source node. Source node is the node from which you will start the breadth first search.

The core principle of BFS is to explore nodes level-by-level. Here's how it works:

• Start with a starting node: This is your entry point into the graph or tree.
• Explore the neighbors: Visit all the nodes directly connected to the starting node.
• Move to the next level: Add all the unexplored neighbors of the visited nodes to a queue (like a waiting line).
• Repeat steps 2 and 3: Take the next node from the queue, explore its neighbors, and add their unexplored neighbors to the queue. This process continues until all nodes have been explored.
• By following this level-by-level approach, BFS guarantees that you'll discover all nodes reachable from the starting node and find the shortest path between them if the graph is unweighted

Breadth first search is a fundamental alogrithm which you should know if you are preparing for coding interviews of tech companies. It is used for solving both easy as well as advanced level problems on Graphs.

Breadth First Search Example

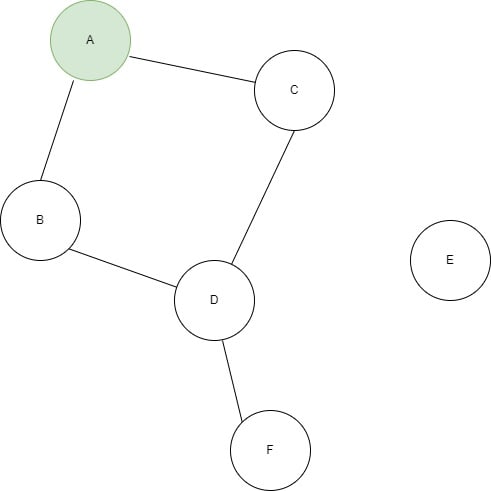
Let's look at the following graph

In the above graph if the source node is node A, then BFS will explore the nodes in the following order:

• Start with the starting node, which is node A.
• Add node A to the queue and mark it as visited.
• Explore the unvisited neighbors of node A, which are nodes B and C. Add them to the queue and mark them as visited.
• Dequeue the next node from the queue, which is node B.
• Explore the unviisted neighbors of node B, which is node D. Add them to the queue and mark them as visited.
• Dequeue the next node from the queue, which is node C.
• Explore the unvisited neighbor of node C, which is nothing since node D has already been visited
• Dequeue the next node from the queue, which is node D.
• Explore the unvisited neighbor of node D, which is node F. Add it to the queue and mark it as visited.
• Dequeue the next node from the queue, which is node F. Since node F has no unvisited neighbors, it is the end of the exploration.

In the above example, since there is no way to reach node E, node E will remain unexplored.

BFS Algorithm Steps

• Step 1: Create an empty queue to store the nodes to be visited and a boolean vector to track the visited nodes. Initially, no node is visited.
• Step 2: Choose a starting node, mark it visited, and add it to the queue.
• Step 3: Extract the front item of the queue, add it to the BFS order, and traverse through the list of that node's adjacent nodes.
• Step 4: If a node in that list has not been already visited, mark it visited, and add it to the back of the queue.
• Step 5: Keep repeating steps 3 and 4 until the queue is empty.

Benefits of Breadth First Search

• Guaranteed to find the shortest path: In unweighted graphs, BFS always finds the shortest path between the starting node and any other node.
• Efficient for dense graphs: BFS shines in graphs with many connections between nodes, as it explores all neighbors efficiently.
• Easy to implement: The basic algorithm is straightforward to understand and code.

Applications of BFS

• Social network analysis: Finding friends of friends or recommended connections on social media platforms.
• Routing algorithms: Finding the shortest path for a delivery truck or navigation app.
• Game playing: AI players in games like chess or Go use BFS to explore possible moves.
• Circuit analysis: Identifying connected components in electrical circuits.

BFS Implementation In Java

public static <T> List<T> bfs(Graph<T> graph, T startNode) {
  Queue<T> queue = new LinkedList<>();
  Set<T> visited = new HashSet<>();

  queue.add(startNode);
  visited.add(startNode);

  List<T> result = new ArrayList<>();

  while (!queue.isEmpty()) {
    T currentNode = queue.poll();
    result.add(currentNode);

    for (T neighbor : graph.getNeighbors(currentNode)) {
      if (!visited.contains(neighbor)) {
        queue.add(neighbor);
        visited.add(neighbor);
      }
    }
  }

  return result;
}

BFS Implementation In Python

from collections import deque

def bfs(graph: Graph, start_node: T) -> List[T]:
    queue = deque([start_node])
    visited = {start_node}

    result = []

    while queue:
        current_node = queue.popleft()
        result.append(current_node)

        for neighbor in graph.get_neighbors(current_node):
            if neighbor not in visited:
                queue.append(neighbor)
                visited.add(neighbor)

    return result

BFS Implementation In C++

std::vector<char> bfs(char start) {
  std::queue<char> queue;
  std::unordered_set<char> visited;

  queue.push(start);
  visited.insert(start);

  std::vector<char> result;

  while (!queue.empty()) {
    char current = queue.front();
    queue.pop();
    result.push_back(current);

    for (char neighbor : graph[current - 'A']) {
      if (!visited.count(neighbor)) {
        queue.push(neighbor);
        visited.insert(neighbor);
        markVisited(neighbor); // Mark neighbour as visited after adding to queue
      }
    }
  }

  return result;
}

BFS Implementation In Javascript

function bfs(graph, start) {
  const queue = [];
  const visited = new Set();

  queue.push(start);
  visited.add(start);

  const result = [];

  while (queue.length) {
    const current = queue.shift();
    result.push(current);

    for (const neighbor of graph.getNeighbors(current)) {
      if (!visited.has(neighbor)) {
        queue.push(neighbor);
        visited.add(neighbor);
      }
    }
  }

  return result;
}