Sorting
In this post we talk about all the common sorting algorithms along with their detailed implementation along with time and space complexity.
Bubble Sort
Bubble sort is an algorithm in which all the elements are traversed one by one and compared with the adjacent element and then swapped according to the order specified. The order can be ascending or descending.
All the elements are compared one by one and sorted based on their values.
For an array of size N, the process has to be repeated N-1 times.
Implementation
Steps
-
Starting with the first element, that is the first index
-
Compare the first element with the next element in the array.
-
If the first element is greater than the second element, swap them.
-
If the above condition fails, move to the next element.
-
Now, compare the second and third elements. If they are not in order, swap them
- Continue the above process until the last element.
Taking the array : {6, 2, 7, 3, 4, 3}
First iteration of bubble sort is shown :
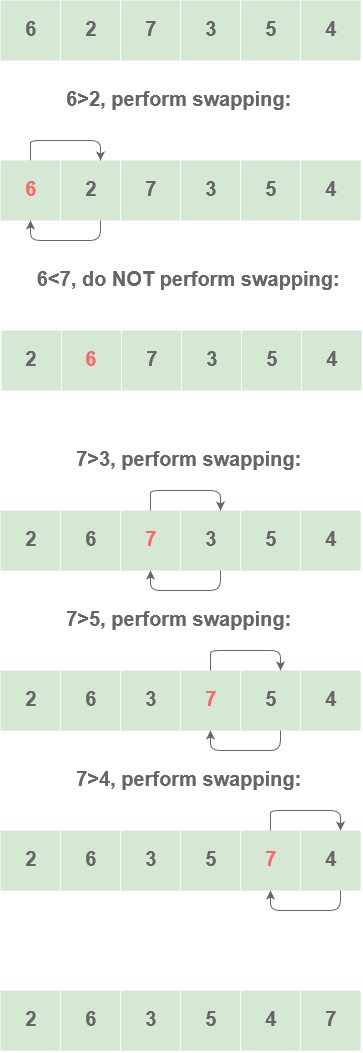
Perform the same process for the remaining iterations.
At the end of each iteration, the largest element gets placed at the end.
In each iteration, the comparison takes place up to the last element.
Code
void BubbleSort(int A[],int size)
{ int i,j,temp;
for (i=0;i<size;i++)
{
for (j=0;j<size-i-1;j++)
{
if(A[j]>A[j+1])
{
temp = A[j];
A[j]= A[j+1];
A[j+1]= temp;
}
}
}
}
Complexity: O(n^2)
Since there are 2 loops running for O(n) time, the complexity is O(n)*O(n) = O(n^2)
Selection Sort
Selection sort is an algorithm in which the smallest element from an unsorted list is selected in each iteration and placed at the beginning of the unsorted list.
Selection sort then selects the next-smallest element every time and swaps it into the correct place. This is why it is called selection sort
Select Sort Implementation
Steps
- Set the first element as
min. - Find the smallest element in the array and assign its index to
min - After each iteration, position the element at
minto the front of the unsorted list.- Start each iteration from the first unsorted element.
- Repeat the first three steps until list is sorted
Example :

Code
void SelectionSort(int A[], int size)
{
for (int i = 0; i < size - 1; i++)
{
int min = i;//stores index of element with minimum value
for (int j = i + 1; j < i; j++)
{
if (A[j] < A[min])
min = j;
}
temp = A[min];
A[min]= A[j];
A[j] = temp;
}
}
Time Complexity : O(N^2)
Since there are 2 loops each running for O(n) , the complexity is O(N)*O(N) = O(N^2).
Insertion Sort
Insertion sort is a sorting algorithm in which an unsorted element is placed at the correct position in each iteration, that is, to the position to which it belongs in a sorted array.
Insertion sort is efficient as it reduces its total number of steps if a partially sorted array is provided as input.
Steps
- Store the second element of the array separately in
key. - Compare
keywith the first element. - If
keyis less than the first element, insert it before the first element else insert it after the first element. - Now, move to the third element and compare it with the elements to the left of it and then insert it in the correct position after comparison.
- Repeat the process until the entire array is sorted.
Visualisation of insertion sort with array = {6, 2, 7, 3, 5, 4} :
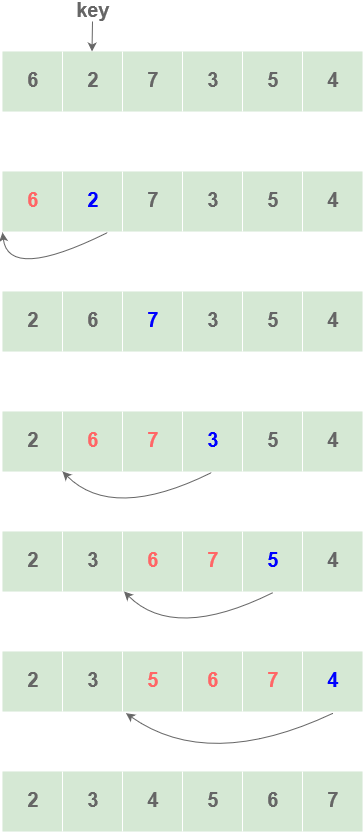
Code
void InsertionSort(int A[], int size) { for (int i = 1; i < size;i++) { int key = A[i]; int j = i - 1; while (key < A[j] && j >= 0) { A[j + 1] = A[j]; --j; } A[j + 1] = key; } }
Each element is compared with all the other elements in the sorted array. For N elements , there will be N^2 comparisons in the worst case. Therefore, the time complexity will be O(N^2) in the worst case
If the array is already sorted, then the time complexity will be O(n)
Quick Sort
Quicksort is a highly efficient sorting algorithm in which a list or array of elements is partitioned into smaller arrays.
A pivot(or central) element is selected in the array. The pivot element can be the first element, the last element, or any random element. The elements smaller than the pivot element are put to its left and greater elements to its right.
Implementation
Steps :
- Fix a pointer at the pivot element. Compare it with the elements starting with the first index. Set a second pointer for the greatest element.
- Set a third pointer to compare the pivot element with all the other elements. If an element smaller than the pivot element is found, swap the smaller element with the greater element.
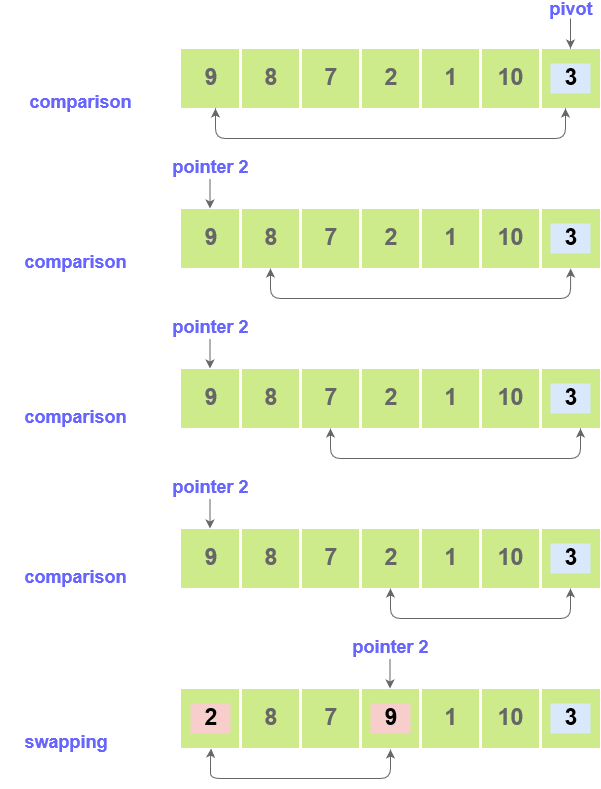
- This process is continued til the second last element is reached.
The pivot element is then swapped with the second pointer.
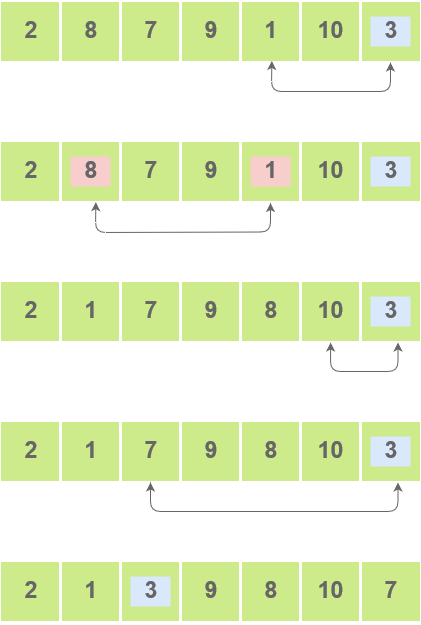
- Pivot elements are again chosen for each of the created sub arrays separately. These pivot elements are then placed at the their correct position. The elements smaller than the pivot element are then put on the left and the elements greater than the pivot element are put on the right.
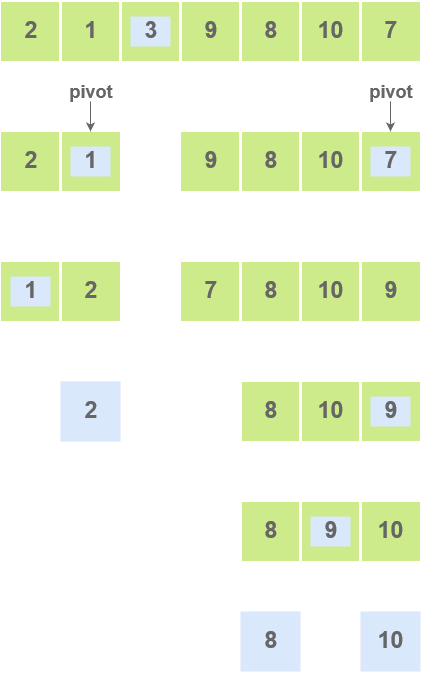
- The sub arrays are further divided into smaller subarrays until a single element sub array is created.
- The array is now sorted
Code:
// partition the A on the basis of pivot element
int partition(int A[], int start, int end) {
int pivot = A[end];
int i = (start - 1);
for (int j = start; j < end; j++) {
if (A[j] <= pivot) {
i++;
swap(&A[i], &A[j]);
}
}
printA(A, 7);
cout << "........\n";
swap(&A[i + 1], &A[end]);
return (i + 1);
}
void QuickSort(int A[], int start, int end) {
if (start < end) {
// Select pivot position and put all the elements smaller than pivot on left and greater than pivot on right
int p = partition(A, start, end);
// Sort the elements on the left of pivot
QuickSort(A, start, p - 1);
// Sort the elements on the right of pivot
QuickSort(A, p + 1, end);
}
}
Time Complexity : O(n^2)
Merge Sort
Merge sort is a sorting algorithm that works on the principle of Divide and Conquer. The array or list of elements is repeatedly broken down into several subarrays until each subarray consists of a single element. Then these subarrays are merged in a way such that the result is a sorted list.
Since the merge sort algorithm uses recursion to sort a given set of elements, it consumes less time.
Steps
- Store the starting index of thearray in
pand store the last index inr. - Store the middle index of array in
q=(p + r)/2 - Break the array into two subarrays, from
ptoqand fromq + 1torindex. - Divide these 2 subarrays again, just like the main array was divided.
- Continue dividing into subarrays until subarrays of single elements get created.
- Now start merging the arrays.
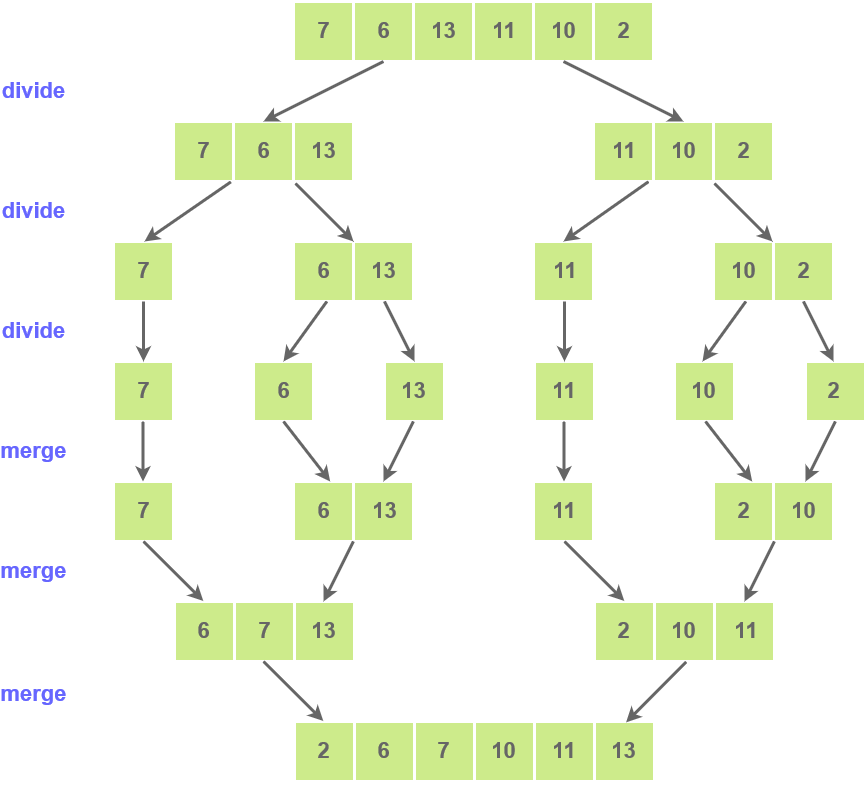
Code
void MergeSort(int A[], int p, int r)
{
int q;
if(p < r)
{
q = (p + r) / 2;
MergeSort(A, p, q);
MergeSort(A, q+1, r);
merge(A, p, q, r);
}
}
// function to merge the subarrays
void merge(int A[], int p, int q, int r)
{
int B[5]; //sAme size of A[]
int i, j, k;
k = 0;
i = p;
j = q + 1;
while(i <= q && j <= r)
{
if(A[i] < A[j])
{
B[k] = A[i];
k++;
i++;
}
else
{
B[k++] = A[j++];
}
}
while(i <= q)
{
B[k++] = A[i++];
}
while(j <= r)
{
B[k++] = A[j++];
}
for(i=r; i >= p; i--)
{
A[i] = B[--k];
}
}